Tóm tắt kiến thức và Giải bài bác 1,2,3,4 trang 26; Bài 5,6,7,8 trang 27 SGK hình học tập 10: Hệ trục tọa độ – Chương 1 Véctơ. Bạn đang xem: Giải sgk toán hình 10
A. Cầm tắt kỹ năng và kiến thức hệ trục tọa độ
1. Trục cùng độ lâu năm đại số trên trục
a) Trục tọa độ: Trục tọa độ là 1 trong đường thẳng trên kia đã xác định một điểm gốc O cùng một vec tơ đơn vị →e
b) Tọa độ của một điểm: Ứng với mỗi điểm M trên trục tọa độ thì có một số thực k sao cho →OM = k = →e
Số k được điện thoại tư vấn là tọa độ của điểm M so với trục đã cho.
c) Độ lâu năm đại số: cho hai điểm A,B bên trên trục số, mãi mãi duy nhất một trong những a sao cho →AB = a→e
a được điện thoại tư vấn là độ lâu năm đại số của vectơ →AB, kí hiệu a = →AB.
Chú ý:
– giả dụ vectơ →AB cùng phía với vec tơ solo vị →e của trục thì ‾AB > 0, còn nếu →AB ngược hướng với vec tơ đối chọi vị →e thì ‾AB →i; →j) bao gồm hai trục (0; →i) và (0;→j) vuông góc với nhau.
O là cội tọa độ (0; →i) là trục hoành
(0;→j) là trục tung |→i| = |→j|= 1
Mặt phẳng được đồ vật một hệ tọa độ được gọi là phương diện phẳng tọa độ
b) Tọa độ vectơ →u = x→i + y→j ⇔ u = (x; y)
hai vectơ đều bằng nhau khi và chỉ còn khi các tọa độ tương ứng bằng nhau →u = (x; y) ; →u’ = (x’; y’)
→u =→u’ ⇔ x = x’
và y = y’
c) Tọa độ một điểm: Với mỗi điểm M trong phương diện phẳng tọa độ thì tọa độ của vec tơ →OM được call là tọa độ của điểm M.→OM = x→i + y→j ⇔ M(x;y)
d) contact giữa tọa độ của điểm với của vectơ:
cho hai điểm A(xA; yA), B(xB;yB)
Ta có →AB = (xA – xB; yA – yB)
Tọa độ của vec tơ thì bởi tọa độ của điểm ngọn trừ đi tọa độ tương xứng của điểm đầu.
3. Tọa độ của tổng, hiệu ,tích của một vài với một vectơ
Cho nhị vec tơ →u = (u1;u2), →v = (v1; v2)
Ta có →u + →v = (u1+ v1; u2 + v2)
→u – →v = (u1- v1; u2 – v2)
k.→u = = (ku1; ku2).
4. Tọa độ của trung điểm của đoạn thẳng cùng tọa độ trung tâm của tam giác
a) Tọa độ trung điểm: đến hai điểm A(xA; yA), B(xB;yB) tọa độ của trung điểm I (xI; yI) được tính theo công thức:
xI = 1/2 (xA + xB) yI = 1/2 (yA + yB).
b) Tọa độ trọng tâm: Tam giác ABC tất cả 3 đỉnh A(xA; yA), B(xB;yB); C(xC; yC). Giữa trung tâm G của tam giác tất cả tọa độ:
xG = 1/3 (xA + xB + xC) yG = 1/3 (yA + yB + yC).
B. Hướng dẫn giải bài bác tập SGK Toán hình học tập lớp 10 trang 26,27
Bài 1.Trên trục (O, →e ) cho những điểm A, B, M gồm tọa độ theo lần lượt là -1, 2, 3, -2 .
a) Hãy vẽ trục và biểu diễn những điểm đã mang lại trên trục;
b) Tính độ dài đại số của →AB và →MN . Từ kia suy ra nhì vectơ →AB và →MN ngược hướng.
Giải: a) Vẽ trục và biểu diễn những điểm đã đến trên trục
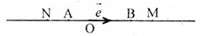
b)Ta có: ‾AB = 2 – (-1) = 3; ‾MN = -2-3= -5. Từ trên đây ta gồm →AB= 3→e, →MN= -5→e với suy ra →AB =-3/5→MN => vectơ →AB và →MN là nhì vectơ ngược hướng.
Xem thêm: Phần Mềm Download Video Trên Web Bất Kỳ Về Máy Tính (Update 2021)
Bài 2.Trong phương diện phẳng tọa độ những mệnh đề sau đúng hay sai?
a) →a = ( -3; 0) và →i = (1; 0) là hai vectơ ngược hướng;
b) →a = ( 3; 4) và →i = (-3; -4) là nhị vectơ đối nhau;
c) →a = ( 5; 3) và →i = (3; 5) là nhị vectơ đối nhau;
d) nhì vec tơ đều bằng nhau khi còn chỉ khi chúng bao gồm hoành độ cân nhau và tung độ bởi nhau
Giải: Các em hãy biểu diễn những véctơ trên mặt phẳng tọa độ
a) Đúng
b) Đúng
c) Sai: hai vectơ →a = ( 5; 3) và →i = (3; 5) không thuộc phương nên không thể đối nhau, thế nên câu c) sai
d) Đúng
Bài 3. Tìm tọa độ của những vec tơ sau:
a) →a = 2→i ; b) →b = -3→j
c) →c = 3→i – 4→j d) →d = 0,2→i + √3→j
Đáp án: a) Ta có : →a = 2→i = 2→i + 0→j ⇒ →a = = (2;0)
b) Ta có: →b = -3→j = 0→i + (-3)→j ⇒ →b = (0; -3)
c) Ta có: →c = 3→i – 4→j = 3→i + (-4)→j ⇒→c = (3; -4)
d) →d = 0,2→i + √3→j = 0,2→i +√3→j ⇒→d = (0,2; √3)
Bài 4. Trong mặt phẳng Oxy. Các khẳng định sau đúng xuất xắc sai?
a) Tọa độ của điểm A là tọa độ của vec tơ →OA;
b) Điểm A nằm trong trục hoành thì bao gồm tung độ bởi 0;
c) Điểm A nằm trong trục tung thì bao gồm hoành độ bằng 0;
d) Hoành độ cùng tung độ của điểm A bằng nhau khi và chỉ còn khi A nằm trong tia phân giác của góc phần bốn thứ nhất.
Đáp án: a) Đúng: Theo khái niệm tọa độ của một điểm
b) Đúng: vì chưng nếu A nằm ở trục hoành và có hoành độ a thì→OA = a→i+ 0→j ⇒ →OA = (a;0) ⇒ A =(a;0)
c) Đúng: do nếu A nằm tại trục tung và gồm tung độ b thì→OA = 0→i+ b→j ⇒ OA = (0;b) ⇒ A =(0;b)
d) Sai. Do đường phân giác của góc phần bốn thứ cha cũng thỏa mãn
Bài 5 trang 27 Hình 10. Trong các mặt phẳng Oxy cho điểm (x0; y0)
a) tra cứu tọa độ điểm A đối xứng với M qua trục Ox;
b) tìm tọa độ điểm B đối xứng cùng với M qua trục Oy;
c) tìm tọa độ điểm C đối xứng cùng với M qua gốc O.
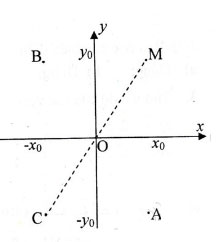
a) hai điểm đối xứng nhau qua trục hoành thì tất cả hoành độ đều nhau và tung độ đối nhau. M0 (x0; y0) ⇒ A(x0;-y0)
b) nhị điểm đối xứng với nhau qua trục tung thì gồm tung độ cân nhau còn hoành độ thì đối nhau. M0 (x0; y0) ⇒ B(-x0;y0)
c) nhì điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau. M0 (x0; y0) ⇒ C(-x0;-y0)
Bài 6. Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4;-1). Search tọa độ điểm D.
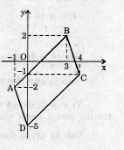
Tứ giác ABCD là hình bình hành nên →CD = →BA
Gọi (x; y) là tọa độ của D thì→CD = (x-4; y+1); →BA = (-4;4);
→CD = →BA ⇔
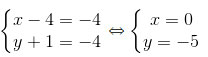
Vậy điểm D(0;-5) là vấn đề cần tìm.
Bài 7 trang 27 Toán hình 10. Các điểm A"(-4; 1), B"(2;4), C(2, -2) lần lượt là trung điểm của những cạnh BC, CA và AB của tam giác ABC. Tìm tọa độ đỉnh của tam giác ABC cùng A’B’C’ trùng nhau.
Giải: A’ là trung điểm của cạnh BC phải -4 = 1/2 (xB+ xC)
⇒ xB+ xC = -8 (1)
Tương trường đoản cú ta tất cả xA+ xC = 4 (2)
xB+ xC = 4 (3)
⇒ xA+ xB+ xC = 0 (4)
Kết hợp (4) và (1) ta có: xA= 8
(4) với (2) ta có: xB= -4
(4) cùng (3) ta có: xC = -4
Tương từ ta tính được: yA = 1; yB = -5; yC = 7.
Vậy A(8;1), B(-4;-5), C(-4; 7).
Gọi G la trọng tâm tam giác ABC thì
xG= (8-4-4)/3= 0; yG = (1-5+7)/3 = 1 ⇒ G(0,1).
xG’= (-4 +2 +2)/3 = 0; yG’ = (1+4-2)/3 = 1⇒ G"(0;1)
Rõ ràng G cùng G’ trùng nhau.
Bài 8. Cho →a = (2; -2), →b = (1; 4). Hãy so với vectơ →c = (5; 0) theo nhị vectơ →a cùng →b.
Giải: Giả sử ta đối chiếu được →c theo →a cùng →b tức là gồm hai số m, n để →c = m.→a + n.→b cho ta →c = (2m+n; -2m+4n)












