GIẢI TOÁN 11 TRANG 36

Hướng dẫn giải, đáp án bài xích 2,3,4,5,6 trang 36,37 SGK giải tích lớp 11(Một số phương trình lượng giác thường xuyên gặp) – Chương 1: Hàm con số giác và phương trình lượng giác.

Bạn đang xem: Giải toán 11 trang 36

Bài 2. Giải những phương trình sau:

a) 2cos2x – 3cosx + 1 = 0 ; b) 2sin2x + √2sin4x = 0.

Đáp án: a) Đặt t = cosx, t ∈ <-1 ; 1> ta được phương trình 2t2 – 3t + 1 = 0 ⇔ t ∈ 1 ; 1/2.

Nghiệm của phương trình đã đến là những nghiệm của nhì phương trình sau:

cosx = 1 ⇔ x = k2π với cosx = 1/2⇔ x = ±π/3 + k2π.

Đáp số : x = k2π ; x = ±π/3 + k2π, k ∈ Z.

b) Ta tất cả sin4x = 2sin2xcos2x (công thức nhân đôi), cho nên phương trình đã cho tương đương với

2sin2x(1 + √2cos2x) = 0 ⇔ 

⇔

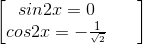
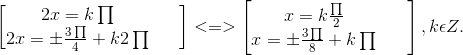
Bài 3. Giải các phương trình sau:

a) sin2 (x/2) – 2cos(x/2) + 2 = 0; b) 8cos2x + 2sinx – 7 = 0;

c) 2tan2x + 3tanx + 1 = 0; d) tanx – 2cotx + 1 = 0.

 a) Đặt t = cos (x/2), t ∈ <-1 ; 1> thì phương trình trở thành

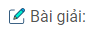
(1 – t2) – 2t + 2 = 0 ⇔ t2 + 2t -3 = 0 ⇔ 

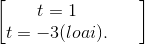
Phương trình vẫn cho tương đương với

cos (x/2) = 1 ⇔ x/2 = k2π ⇔ x = 4kπ, k ∈ Z.

b) Đặt t = sinx, t ∈ <-1 ; 1> thì phương trình trở thành

8(1 – t2) + 2t – 7 = 0 ⇔ 8t2 – 2t – 1 = 0 ⇔ t ∈ 1/2;-1/4.

Các nghiệm của phương trình đã cho rằng nghiệm của hai phương trình sau :

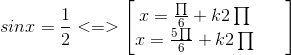
và 

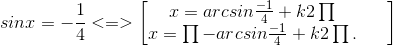
Đáp số : x = π/6 + k2π; x = 5π/6 + k2π;

x = arcsin(-1/4) + k2π; x = π – arcsin(-1/4) + k2π, k ∈ Z.

c) Đặt t = tanx thì phương trình vươn lên là 2t2 + 3t + 1 = 0 ⇔ t ∈ -1 ; -1/2.

Vậy 

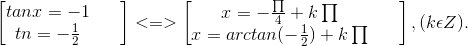
d) Đặt t = tanx thì phương trình trở thành

t – 2/t + 1 = 0 ⇔ t2 + t – 2 = 0 ⇔ t ∈ 1 ; -2.

Vậy 

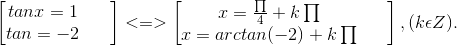
Bài 4: Giải các phương trình sau:

a) 2sin2x + sinxcosx – 3cos2x = 0;

b) 3sin2x – 4sinxcosx + 5cos2x = 2;

c) 3sin2x – sin2x + 2cos2x = 1/2 ;

d) 2cos2x – 3√3sin2x – 4sin2x = -4.

Giải: a) dễ thấy cosx = 0 không thỏa mãn phương trình đã cho nên vì vậy chiaw phương trình cho cos2x ta được phương trình tương đương 2tan2x + tanx – 3 = 0.

Xem thêm: Thuyết Minh Tình Đầu Khó Phai, Tình Đầu Khó Phai Tập 591 Thvl1

Đặt t = tanx thì phương trình này trở thành

2t2 + t – 3 = 0 ⇔ t ∈ 1 ; -3/2.

Vậy 

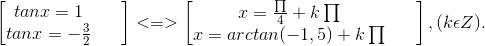
b) gắng 2 = 2(sin2x + cos2x), phương trình đã mang đến trở thành

3sin2x – 4sinxcosx + 5cos2x = 2sin2x + 2cos2x

⇔ sin2x – 4sinxcosx + 3cos2x = 0

⇔ tan2x – 4tanx + 3 = 0

⇔ 

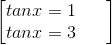
⇔ x = Π/4 + kπ ; x = arctan3 + kπ, k ∈ Z.

c) cố gắng sin2x = 2sinxcosx ;

1/2=1/2(sin2x + cos2x) vào phương trình đã cho và rút gọn gàng ta được phương trình tương đương

1/2 sin2x + 2sinxcosx – 5/2cos2x = 0 ⇔ tan2x + 4tanx – 5 = 0 ⇔ 

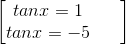
⇔ x = π/4 + kπ ; x = arctan(-5) + kπ, k ∈ Z.

d) 2cos2x – 3√3sin2x – 4sin2x = -4

⇔ 2cos2x – 3√3sin2x + 4 – 4sin2x = 0

⇔ 6cos2x – 6√3sinxcosx = 0 ⇔ cosx(cosx – √3sinx) = 0

⇔ 

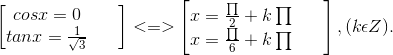
Bài 5. Giải các phương trình sau:

a) cosx – √3sinx = √2; b) 3sin3x – 4cos3x = 5;

c) 2sin2x + 2cos2x – √2 = 0; d) 5cos2x + 12sin2x -13 = 0.

Giải: a) cosx – √3sinx = √2 ⇔ cosx – tan π/3sinx = √2

⇔ cos π/3cosx – sinπ/3sinx = √2cosπ/3⇔ cos(x +π/3) = √2/2

⇔

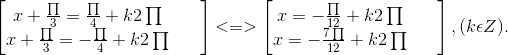
b) 3sin3x – 4cos3x = 5 ⇔ 3/5sin3x – 4/5cos3x = 1.

Đặt α = arccos thì phương trình trở thành

cosαsin3x – sinαcos3x = 1 ⇔ sin(3x – α) = 1 ⇔ 3x – α = π/2 + k2π

⇔ x = π/6 +α/3 +k(2π/3) , k ∈ Z (trong đó α = arccos3/5).

c) Ta gồm sinx + cosx = √2cos(x – π/4) buộc phải phương trình tương tự với 2√2cos(x – π/4) – √2 = 0 ⇔ cos(x – π/4) = 1/2

⇔

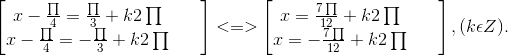
d) 5cos2x + 12sin2x -13 = 0 ⇔ 

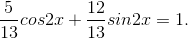
Đặt α = arccos5/13 thì phương trình trở thành

cosαcos2x + sinαsin2x = 1 ⇔ cos(2x – α) = 1

⇔ x = α/2 + kπ, k ∈ Z (trong đó α = arccos 5/13).

Bài 6. a. Tan (2x + 1)tan (3x – 1) = 1;

b. Chảy x + rã (x + π/4) = 1

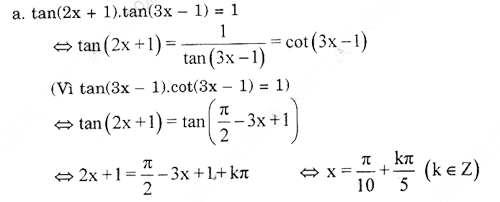
Ôn lại Lý thuyết

Phương pháp giải phương trình bậc nhất đối với cùng một hàm số lượng giác

Chỉ buộc phải thực hiên nhị phép đổi khác tương đương: dịch số hạng không đựng x lịch sự vế đề nghị và đổi dấu; phân chia hai vế phương trình cho một trong những khác 0 là ta hoàn toàn có thể đưa phương trình lượng giác cơ bạn dạng đã biết cách giải.

Phương pháp giải phương trình bậc hai so với một hàm con số giác

Đặt hàm con số giác đựng ẩn phụ ta gửi được phương trình về dạng một phương trình bậc hai. Giải phương trình bậc nhị này. Giả dụ phương trình bậc hai gồm nghiệm thì cố gắng giá trị của nghiệm kiếm được trở lại phép đặt ta sẽ tiến hành một phương trình lượng giác cơ bạn dạng đã biết phương pháp giải.

Phương pháp giải phương trình asinx + bcosx = c

Chỉ yêu cầu xét trường thích hợp cả hai hệ số a, b đông đảo khác 0 (trường hợp một trong những hai thông số đó bằng 0 thì phương trình phải giải là hpuwong trình số 1 đối với 1 hàm con số giác (sinx hoặc cosx) đã hiểu phương pháp giải.

Cách 1: chia hai vế phương trình cho

 và gọi α là góc lượng giác tạo do chiều dương của trục hoành cùng với vecto OM = (a ; b) thì phương trình biến hóa một phương trình đã hiểu cách thức giải:Cách 2: Viết lại phương trình dưới dạng, phương trình biến :

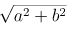
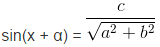
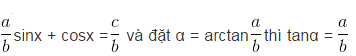
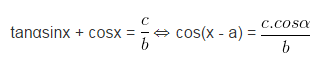
Phương trình này đã biết phương pháp giải.

Chú ý : Để phương trình 

 có nghiệm, điều kiện cần với đủ là

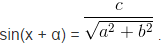
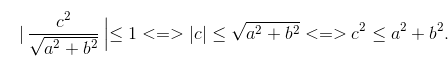
Đó cũng là điều kiện cần cùng đủ để phương trình asinx + bcosx = c có nghiệm.

Phương pháp giải những phương trình đưa được về dạng phương trình bậc nhất, bậc hai đối với một hàm con số giác

Hệ thống các công thức lượng giác rất nhiều chủng loại nên các phương trình lượng giác cũng khá đa dạng. áp dụng thành thạo những phép chuyển đổi lượng giác những em rất có thể đưa những phương trình phải giải về dạng phương trình bậc nhất, bậc hai đối với một hàm số lượng giác. Chẳng hạn, phương trình đẳng cấp bậc hai so với cosx với sinx :

a.sin2x + b.sinx.cosx + cos2x = d

có thể mang đến dạng phương trình bậc hai đối với tanx bằng cách chia phương trình cho cos2x. Bởi vì sự phong phú và đa dạng và đa dạng mẫu mã ấy nên cửa hàng chúng tôi cũng chỉ rất có thể minh họa phương pháp giải thông qua một số trong những ví dụ điển hình và những em có thể nắm vững phương pháp giải thông qua nhiều bài bác tập.