Hàm số lượng giác và phương trình lượng giác

Bài viết này của h3qvn.com sẽ phân tách sẻ chi tiết các kỹ năng và kiến thức từ cơ bản đến nâng cấp của hàm số lượng giác trong toán học. Vấn đề này để giúp bạn dễ dãi tổng hợp, cũng giống như ghi nhớ giỏi hơn những kiến thức vẫn học bên trên trường lớp.

Bạn đang xem: Hàm số lượng giác và phương trình lượng giác

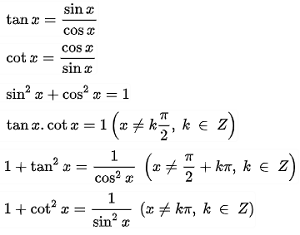
2.2 phương pháp cộng vào hàm số lượng giác

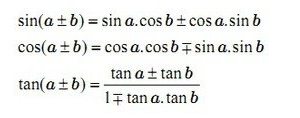
Mẹo dùng để làm nhớ nhanh những công thức cộng trong hàm số là lời nói “Sin thì sin cos cos sin, cos thì cos cos sin sin vệt trừ. Chảy thì chảy nọ tung kia phân chia cho mẫu tiên phong hàng đầu trừ tung tan.”

2.3 Công thức những cung liên quan trên phố tròn lượng giác

Hai góc đối nhau:

cos (-x) = cos x

sin (-x) = -sin x

tan (-x) = -tan x

cot (-x) = -cot x

Hai góc bù nhau:

sin (π - x) = sin x

cos (π - x) = -cos x

tan (π - x) = -tan x

cot (π - x) = -cot x

Hai góc phụ nhau:

sin (π/2 - x) = cos x

cos (π/2 - x) = sin x

tan (π/2 - x) = cot x

cot (π/2 - x) = rã x

Hai góc hơn yếu π:

sin (π + x) = -sin x

cos (π + x) = -cos x

tan (π + x) = tan x

cot (π + x) = cot x

Hai góc hơn yếu π/2:

sin (π/2 + x) = cos x

cos (π/2 + x) = -sin x

tan (π/2 + x) = -cot x

cot (π/2 + x) = -tan x

Mẹo nhớ nhanh phương pháp như sau: “Cos đối, sin bù, phụ chéo, rã hơn kém π.”

2.4 bí quyết nhân

2.5 cách làm hạ bậc trong hàm số lượng giác

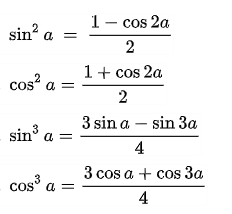
2.6 cách làm biến tổng thành tích

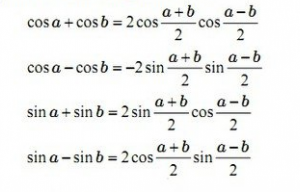
Mẹo giúp dễ dàng ghi nhớ công thức hơn: “Cos cùng cos bởi 2 cos cos, cos trừ cos bởi trừ 2 sin sin; sin cộng sin bởi 2 sin cos, sin trừ sin bởi 2 cos sin.”

2.7 công thức biến tích thành tổng

2.8 Nghiệm của phương trình lượng giác

Phương trình lượng giác cơ bản:

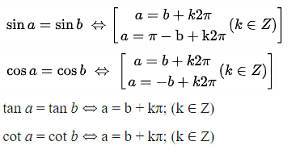
Phương trình lượng giác vào trường hợp sệt biệt:

sin a = 0 ⇔ a = kπ; (k ∈ Z)

sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)

sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)

cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)

cos a = 1 ⇔ a = k2π; (k ∈ Z)

cos a = -1 ⇔ a = π + k2π; (k ∈ Z)

3. Phương trình lượng giác cơ bản và các trường hợp đặt biệt

3.1 Phương trình sin x = sin α, sin x = a

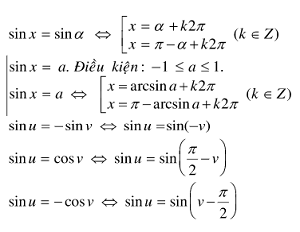
Các trường hợp sệt biệt:

3.2 Phương trình cos x = cos α, cos x = a

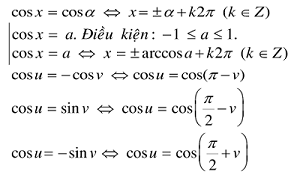
Các trường hợp đặc biệt:

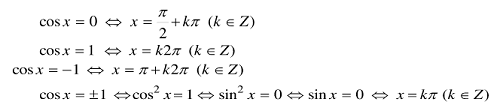
3.3 Phương trình tung x = chảy α, chảy x = a

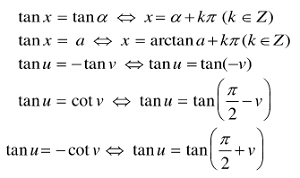
Các ngôi trường hợp sệt biệt:

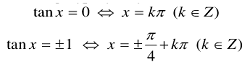
3.4 Phương trình cot x = cot α, cot x = a

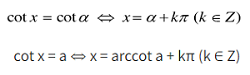
Các ngôi trường hợp quánh biệt:

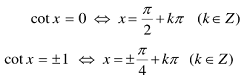
3.5 Phương trình số 1 đối với cùng một hàm số lượng giác

Có dạng at + b = 0 cùng với a, b ∈ Ζ, a ≠ 0,với t là một trong hàm con số giác nào đó. Công thức giải như sau:

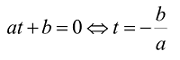
4. Đạo hàm hàm con số giác cơ bản

Đạo hàm của các hàm lượng giác là phương thức toán học tập tìm tốc độ biến thiên của một hàm số lượng giác theo sự thay đổi thiên của trở thành số. Các hàm số lượng giác thường gặp mặt là sin(x), cos(x) và tan(x).

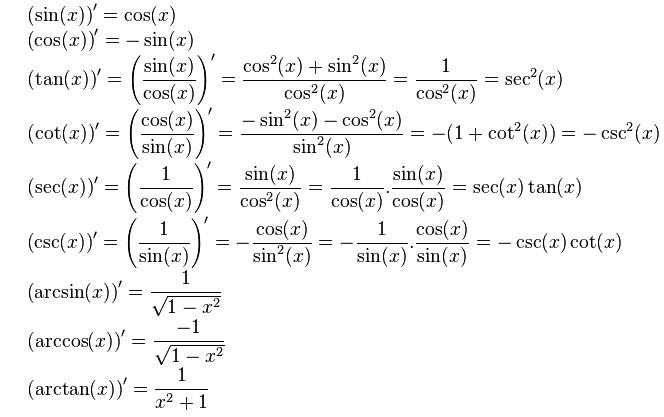
5. Cách tính giới hạn hàm con số giác tuyệt nhất

Áp dụng giới hạn đặc biệt:

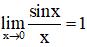
Các bước tìm số lượng giới hạn hàm con số giác của

Bước 1: Sử dụng các công thức lượng giác cơ bản, phương pháp nhân đôi, công thức cộng, cách làm biến đổi,… để thay đổi hàm con số giác f(x) về thuộc dạng giới hạn đặc trưng nêu trên.

Bước 2: Áp dụng những định lý về số lượng giới hạn để tìm số lượng giới hạn đã cho.

6. Phương pháp tính chu kỳ hàm con số giác dễ dàng nắm bắt nhất

Hàm số y= f(x) xác minh trên tập thích hợp D được hotline là hàm số tuần hoàn nếu có số T ≠ 0 làm thế nào để cho với gần như x ∈ D ta tất cả x+T ∈ D;x-T ∈ D cùng f(x+T)=f(x). Nếu gồm số T dương bé dại nhất vừa lòng các đk trên thì hàm số đó được gọi là 1 trong hàm số tuần trả với chu kì T.

Xem thêm: Máy Cắt Củ Quả Đa Năng Nào Trên Thị Trường? Máy Cắt Rau Củ Quả Đa Năng

Cách search chu kì của hàm số lượng giác (nếu có):

Hàm số y = k.sin(ax+b) tất cả chu kì là T= 2π/|a|

Hàm số y= k.cos(ax+ b) bao gồm chu kì là T= 2π/|a|

Hàm số y= k.tan( ax+ b) gồm chu kì là T= π/|a|

Hàm số y= k.cot (ax+ b ) bao gồm chu kì là: T= π/|a|

Hàm số y= f(x) bao gồm chu kì T1; hàm số T2 có chu kì T2 thì chu kì của hàm số y= a.f(x)+ b.g(x) là T = bội chung nhỏ tuổi nhất của T1 với T2

Bài tập mẫu:

Trong các hàm số sau đây, hàm số như thế nào là hàm số tuần hoàn?

A. Y= sinx- x

B. Y= cosx

C. Y= x.sin x

D. Y=(x2+1)/x

Đáp án: chọn B

Tập khẳng định của hàm số: D=R .

mọi x ∈ D , k ∈ Z ta bao gồm x-2kπ ∈ D và x+2kπ ∈ D,cos(x+2kπ)=cosx .

Vậy y= cosx là hàm số tuần hoàn.

Trên đây là tất cả những thông tin về hàm số lượng giác mà bạn phải ghi nhớ. Hy vọng, với những share thực tế trên phía trên của h3qvn.com, sẽ giúp bạn dễ dàng chinh phục các đề thi sắp đến tới. Xin được đồng hành cùng bạn.