Bạn đang xem: Số chính phương lớp 6
Bởi các kiến thức tương quan đến số thiết yếu phương đã được học tự lớp 8 thậm chí là là lớp 6 nên việc nhớ lại những kiến thức này hơi là khó. Đừng lo lắng nội dung bài viết này để giúp đỡ bạn bổ sung thêm những kiến thức cần thiết liên quan mang đến số chủ yếu phương.Contents
1 Số chủ yếu phương là gì?2 Đặc điểm của số chính phương3 Một vài ví dụ về số chính phương4 một số bài tập ví dụSố bao gồm phương là gì?
Số bao gồm phương hay nói một cách khác là số hình vuông. Đây là số tự nhiên và thoải mái có căn bậc hai là một trong những tự nhiên, có thể nói rằng thì số chính phương bằng bình phương (lũy quá bậc 2) của một trong những tự nhiên. Số chính phương có cách gọi khác là số hình vuông, vì chưng số bao gồm phương là bình phương của một số trong những tự nhiên mà diện tích hình vuông vắn là nhì cạnh nhân nhau (bình phương của một cạnh).
Với các số nguyên thì ta sẽ có: số nguyên dương, nguyên âm cùng số 0.
Ví dụ: 9 ( 3 2 ) ; 16 ( 4 2 ) ; 36 ( 6 2 ) đây chính là số bao gồm phương.

Số chủ yếu phương được chia nhỏ ra làm hai một số loại đó là chẵn và lẻ. Một vài chính phương sẽ được gọi là số chủ yếu phương chẵn khi nó là bình phương của một số trong những chẵn và ngược lại. Một trong những chính phương được điện thoại tư vấn là số bao gồm phương lẻ khi nó là bình phương của một trong những lẻ.
Có nhiều người thắc mắc số 1 có đề nghị là số thiết yếu phương hay không và số chủ yếu phương nhỏ tuổi nhất là số nào? Tận thuộc của số chủ yếu phương thường kết thúc bằng 0, 1, 4, 5, 6, 9 và bắt buộc là các số 2, 3, 7, 8. Thế nên mà số 1 là số chính phương với số chủ yếu phương bé dại nhất là số 0.
Đặc điểm của số chính phương
Để nắm rõ hơn về số thiết yếu phương thì chúng ta đọc hãy tham khảo các đặc điểm dưới đây:
lúc phân tích một số trong những chính phương ra thừa số nhân tố thì ta vẫn được những thừa số là lũy vượt của số thành phần với số nón chẵn. Số chủ yếu phương chỉ tất cả thể có một trong 2 dạng đó là: 4n hoặc 4n + 1 và không có số thiết yếu phương nào gồm dạng là 4n + 2 hoặc 4n + 3 (với n € N). Số bao gồm phương chỉ tất cả thể có 1 trong 2 dạng kia là: 3n hoặc 3n + 1 và không có số thiết yếu phương nào gồm dạng là 3n + 2 (với n € N). Số chủ yếu phương gồm chữ số tận cùng là 1 hoặc 9 thì chữ số hàng chục sẽ là chữ số chẵn. Số chính phương bao gồm tận cùng bằng 5 thì chữ số hàng trăm sẽ là 2.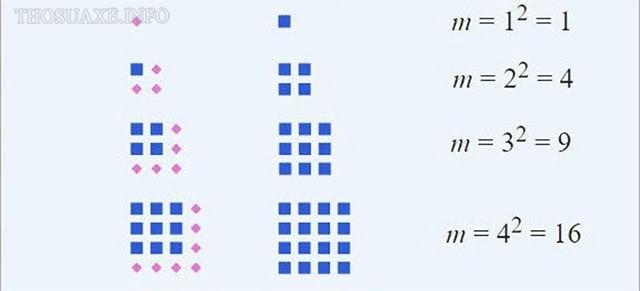
Ví dụ: 81:8 = 10 dư 1.
Số cầu nguyên dương của số chính phương chính là một số lẻ. Số chủ yếu phương phân tách hết cho số nguyên tố phường thì cũng sẽ chia hết mang đến phường 2 .Ví dụ: Số chính phương của 36 bởi 6 2 phân chia hết mang đến 2
=> 36 phân tách hết mang lại 4 ( 2 2 ) .
toàn bộ các số thiết yếu phương đều có thể viết thành dãy tổng của những số lẻ tăng cao từ 1: 1; 1 + 3; 1 + 3 + 5; 1 + 3 + 5 + 7; 1 + 3 + 5 + 7 + 9;…v.vCông thức được dùng để tính hiệu của nhị số bao gồm phương là:
a2 – b2 = (a – b)(a + b).
Ví dụ: 62 – 32 = (6 + 3)(6 – 3) = 9.3 = 27.
Một vài lấy ví dụ như về số chính phương

Dựa trên khái niệm, đặc điểm và tính chất của số chính phương ta có một số trong những ví dụ về số thiết yếu phương như sau:
4 là một vài chính phương chẵn, vì chưng 4 = 2 2 9 là một vài chính phương lẻ, vày 9 = 3 2 16 là một số chính phương chẵn, cũng chính vì 16 = 4 2 25 là một trong những chính phương lẻ, bởi 25 = 5 2 36 là một vài chính phương chẵn, bởi vì 36 = 6 2 225 là một số trong những chính phương lẻ, bởi 225 = 15 2 289 là một vài chính phương lẻ, do 289 = 17 2 576 là một vài chính phương chẵn, vì chưng 576 = 24 2 một triệu là một số chính phương chẵn, vị 1.000.000= 1.000 2Một số bài bác tập ví dụ
Câu 1: Hãy chứng tỏ 1234567890 không hẳn là số bao gồm phương.
Giải:
Ta bao gồm số 1234567890 phân chia hết mang lại 5 bởi vì tận thuộc là số 0 nhưng này lại không phân tách hết mang đến 25. Vì hai số tận cùng là 90.
Vậy đề xuất số 1234567890 không phải là số chính phương.
Câu 2: chứng tỏ một số là số chính phương:
Chứng minh: với tất cả số tự nhiên và thoải mái n thì a n = n(n + 1) (n + 2) (n + 3) + 1 là số chính phương.
Giải:
Ta có: a n = n(n+1)(n+2)(n+3) + 1
= (n 2 + 3n)(n 2 + 3n + 2) +1
= (n 2 + 3n) 2 + 2(n 2 + 3n) + 1
= (n 2 + 3n + 1) 2
Với n là một số tự nhiên thì (n 2 + 3n + 1) 2 cũng trở nên là một trong những tự nhiên. Vậy bắt buộc a n là một vài chính phương.
Câu 3: chứng minh số dưới đây không nên số chủ yếu phương
n = 2004 2 + 2003 2 + 2002 2 – 2001 2
Giải:
Theo như đề bài thì ta tất cả tận cùng của những số lần lượt là 6, 9, 4, 1. Do đó, số tự nhiên và thoải mái n bao gồm chữ số tận thuộc là 8 buộc phải n chưa hẳn là số chủ yếu phương.
Như vậy bài viết trên đây đang vừa chia sẻ cho chúng ta đọc các kiến thức về số bao gồm phương cũng như trả lời đến câu hỏi: “ Số chủ yếu phương là gì?”. Hi vọng những thông tin chia sẻ trên trên đây sẽ cung cấp thêm cho chính mình một số kiến thức ship hàng cho quy trình học tập của mình.












